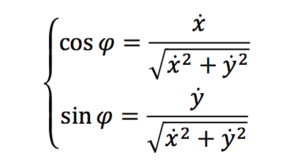【新歓企画】フラットサーブ論争に終止符を打つ！ ?フラットサーブを物理で検証?

こんにちは。須藤です。

新歓用にブログを書くように依頼されてしまいました。しかし私はウィットに富んだ文章を書けるわけではなく、話題探しに困ってしまいました。そもそもこのブログはどのような方が読まれているのでしょうか。正直なところ見当もつきません（当ブログにご訪問いただきありがとうございます！）。ただ、これをご覧になっているということは、少なくともテニスに興味がおありだと思います。というわけでただそれだけの理由ではありますが、今回はテニスをやっている人なら誰でも一度は抱くであろう疑問、「200km/hのフラットサーブを打つにはどれくらいの高さが必要なの？」ということを検証していきたいと思います。一応高校レベルでもわかるように書いていこうと思います。……新歓のことを知りたい方はこの記事を読んでから庭球部HPやTwitter、他の方の記事をご覧ください。

プロ選手を見ていると、当然のように速いサーブをバンバン決めていきますよね。200km/hもの高速サーブを打つ選手も今や特別なことではありません。さて、トッププロの中でもサーブを特に得意としているカルロビッチ選手やイズナー選手は2mを超える長身で日本人からすれば「ずるい！」と思ってしまいます。実際、身長180cm程度の錦織選手は200km/hを超えるサーブを打つことはほとんどありません。それでは、身長の低い日本人が200km/hのサーブを打つことは不可能なのでしょうか？

無回転のフラットサーブをセンターに打つ事を考えてみましょう。一般的な言説として、フラットサーブは直線軌道なので身長が低いとネットに突き刺さってしまうといいます。サービスラインからネット上端をめがけて伸ばした直線はベースラインの遥か上空を通過するから、だそうです。実際、ネットとサービスラインの距離は6.40m、ネットとベースラインの距離は11.885m、ネットの高さは0.914mですから上記の直線はベースラインの2.61m上空を通過します。170cmの人のサーブの打点は2.5m程度ですから確かに身長の低い人の打点からはサービスラインを見ることはできません。

しかし、重力を受けながら空中を運動する物体は放物線を描きます。さらには空気による抵抗も受けるため、放物線軌道で予想される落下点よりも前に落ちます。直線軌道という前提は全く誤りですから、170cm程度の身長でも200km/hのサーブが打てる可能性が見えてきました。

それでは一体どの高さから打てば、高速のフラットサーブをセンターに打ち込むことができるのか検証していきましょう。

※※ここからは物理の計算をします！他の方が検証できるように考え方も記しておきます。物理が苦手な方は結論だけみてください。※※

***********************************************************************

重力ならびに空気抵抗も考えていきます。なおボールは空中にいる間、形の変わらない完全な球（剛体球）であるとし、風や縫い目などに起因する乱流、その他回転の影響は考えないものとします。

ボールがどういう軌道を描くのか計算しましょう。ボールの質量をmとして、速さVで水平より角度θの方向に打ちあげるものとし、水平方向をx軸、鉛直方向をy軸とします。

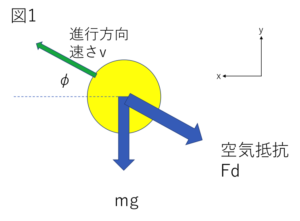
空中に放たれたボールが受ける力は重力と空気抵抗（Fd）の二つです（図１）。

空気抵抗はその大きさが速さの二乗に比例する抵抗（慣性抵抗）のみ考えます（注 速さに比例する粘性抵抗はサーブの状況ではとても小さいため無視します）。球に働く空気抵抗の大きさはより詳しくは次の式で表されます。

Fd=π/2CdρR^2v^2

なお R:半径　ρ:空気の密度　Cd:抵抗係数　v:球の速さ を表します。

さて、ボールの運動方程式は次のようになります。

gは重力加速度、φはボールの進行方向と水平面の成す仰角です。なお表記ですがはそれぞれx方向の速度、加速度を表します。ここでφは

の関係を満たすので運動方程式は次のように書き換えられます。

加速度を二回積分すればボールの軌道がわかりますが、この式は複雑な微分方程式で解けません。というわけで、積分の代わりに台形近似してx、yの値を求めてみたいと思います。どうやるかを簡単に説明すると、初期速度が決まっていますからt=0sでの加速度は計算できるわけです。次に非常に短い時間経過後、例えばt=0.001sでの加速度をt=0sでの速度を代用して計算します。そしてt=0.001sでの速度を上記二つの加速度を用いて計算します。そのあとは全く同じことを繰り返していけばいつまでも計算できるわけです。速度から位置への換算も同じようにやります。Excelを用いてこれらの計算をやりました。

計算に使用した定数たちの値を書いておきます。

m:57.7g　R:3.3cm　ρ:1.2kg/m³　Cd:0.39　g:9.8m/s²

**************************************************************************

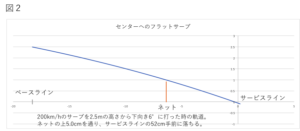
以上のような計算をもとに、初速200km/hでのサーブの軌道を図にしました。図2は高さ2.5mからサーブした時の軌道の一例です。

θが-6°の時（＝下向きに6°の角度で打ち出す時）に200km/hのサーブを入れることができるのです！より具体的には下向きに5.8°?6.2°の方向に打ち出せば、サーブはネットを越え、かつサービスラインの手前に落ちます。許される角度は非常にシビアですが、身長170cmの人でも200km/hのサーブを打つことは可能であるということが示されました。

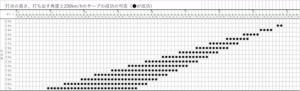
というわけで打ち出す高さを様々に変えて200km/hサーブに許される角度幅を表にまとめました。

なんと、打点高が2.3mあればなんとか200km/hのサーブを入れられるようです！そして打点高が3.3mにもなると(身長2mくらいのビッグサーバーはこのくらいだと予想されます)8.2°?10.1°と許される角度幅が2.5mの場合と比べて4?5倍となっていることがわかります。

いかがだったでしょうか。空気抵抗は空気の密度や温度、気圧によっても変化しますし回転の影響を全く無視していて、近似を多用しているため今回の計算は唯一の正解を示すものではありませんが、大きくずれてはいないと思います。サーブに関してはハイレベルの世界では身長が高い人が圧倒的に有利であることが再確認できましたね。

というわけで日本人体型の皆さんは速いフラットサーブを練習するのではなく、回転系のサーブを習得するのが良さそうです！

質問、ご意見があれば東大庭球部までお問い合わせください。

そしてこの記事を最後まで読んでしまった東大生の君！！

ぜひ練習会へ来てみよう！練習会がやっていない時期でもいつでも体験練習を受け付けています！

庭球部の普段の様子は他の記事をご覧ください（・Θ・）